|
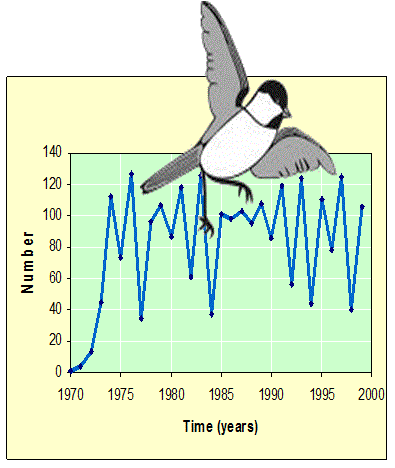
Como o caos emerge
nos modelos determinísticos de crescimento populacional? Quais são as ferramentas quantitativas necessárias para entender
e representar o comportamento caótico?
O modelo logístico
é sado para descrever o crescimento de uma população num ambiente com recursos limitados. Quando uma população cresce continuamente
(ou seja, quando as taxas de natalidade e mortalidade não ocorrem em intervalos fixos) o modelo logístico sempre resulta num
crescimento gradual e previsível da população até um valor limitante, a capacidade de suporte, o valor máximo de indivíduos
que o ambiente pode suportar. Mas, quando a população cresce de forma discreta
(como uma população que reproduz em intervalos fixos – como uma vez por ano na primavera) então a dinâmica pode ser
mais complexa. O modelo pode resultar numa população que alcança um equilíbrio simples, tem oscilações periódicas ou exibe
um comportamento caótico, dependente da taxa de crescimento do intervalo discreto do tempo. Nessa tarefa você usará um intervalo
de tempo de um ano e avaliar explore a dinâmica do modelo logístico discreto com taxas diferentes de crescimento.

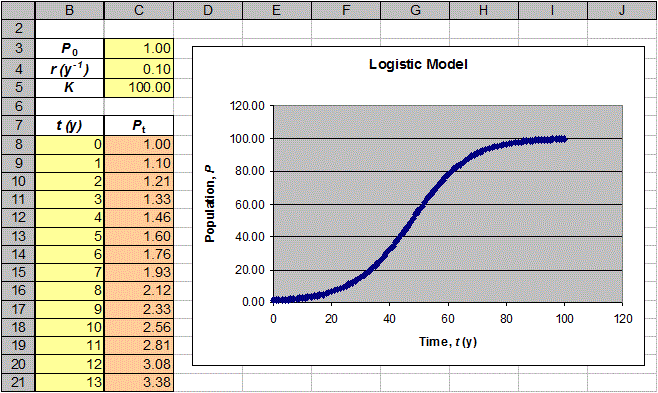
Começamos criando uma planilha da
equação de diferencia do modelo logístico:
DP=rP(1-P/K), onde P
é o tamanho populacional, r é a taxa intrínseca de crescimento e K é a capacidade de suporte. A equação de diferencia
que calcula a população de uma geração a próxima é: Pt+1=Pt
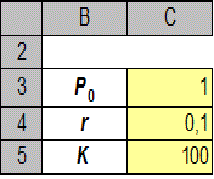
+ DPt , com uma população inicial
de P0 . Neste exemplo começamos com uma população inicial de 1, uma taxa de crescimento de 0.1 por ano e
uma capacidade de suporte de 100.

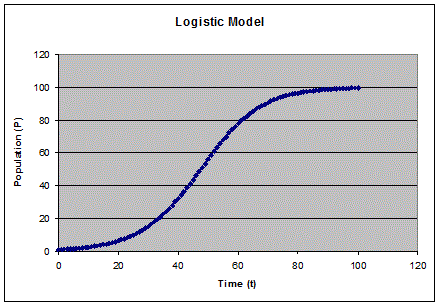
Crie um gráfico da
população como função do tempo prevista no modelo logístico.
Use um gráfico
de dispersão de X e Y com pontos conectados . Nomeie os eixos e formate corretamente o gráfico.
Dica: Para fazer um
gráfico, selecione as colunas dos eixos x e y que quer fazer um gráfico.

Agora podemos explorar
como a solução ao modelo logístico depende dos três parâmetros P0, r e K.
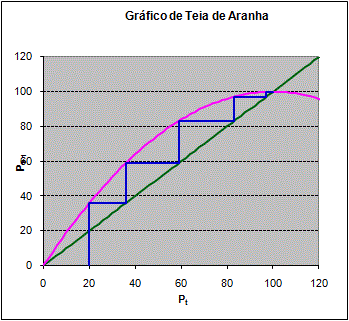
Para entender como
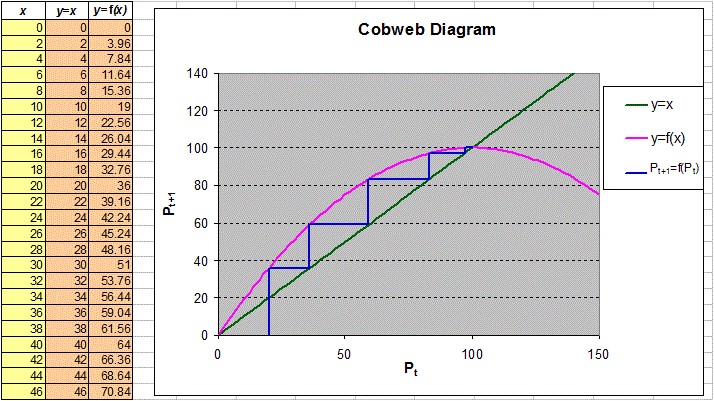
os tipos diferentes de comportamento no modelo logístico aparecem é útil criar um gráfico de teia de aranha. Esse é um gráfico
de Pt+1 contra Pt e é usado para ilustrar como a seqüência
de valores é gerada pela equação de diferencia, Pt+1=f(Pt). Para o modelo logístico, f(x)=x + r x (1-x/K). No gráfico de teia de aranha começamos
com o valor inicial de x= P0, move a curva y=f(x) para obter o valor y=P1 e retorne a linha y=x para
encontrar o próximo valor x= P1.. Repita o processo. A seqüência de pontos para fazer gráficos é (P0,0), (P0,P1), (P1,P1), (P1,P2)
… Veja o gráfico ao kado.

Para criar o gráfico inteiro
de teia de aranha precisa fazer um gráfico da linha, y=x, a curva, y= f(x)=x + r x (1-x/K), e a seqüência de pontos do passo anterior.
Adicione colunas novas na planilha
que permitem fazer um gráfico de y=x e y= f(x)=x + r x (1-x/K). Precisa incluir uma coluna de valores de x,
que devem variar entre 0 e 200 (ou duas vezes a capacidade de suporte). Ao adicionar as, faz um gráfico de y=x
e y= f(x) e Pt+1 contra Pt no mesmo gráfico. Use a dispersão de X e Y com pontos conectadas
para fazer o gráfico. Use cores distintos para cada curva.
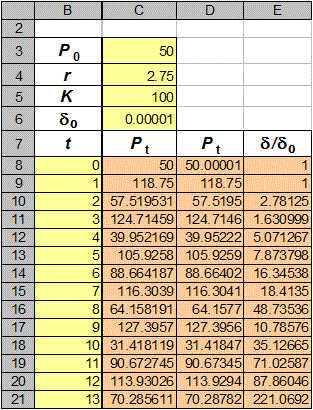
Crie uma copia da primeira planilha
e colar numa planilha nova. Agora crie uma entrada para a diferencia inicial
das populações, d0 .
Adicione uma coluna nova de população,
com o valor inicial é P0+ d0 . Pode formatar as colunas de modo de demonstrar suficientes decimais para
ilustrar a diferencia pequena nas populações.
Finalmente crie uma coluna onde calculará d/d0. Essa coluna somente
precisa aproximadamente 30 passos de tempo. Pode observar que esse valor pula. Mas, observará uma tendência de crescer quando
r está nas regiões onde a dinâmica populacional é caótica.
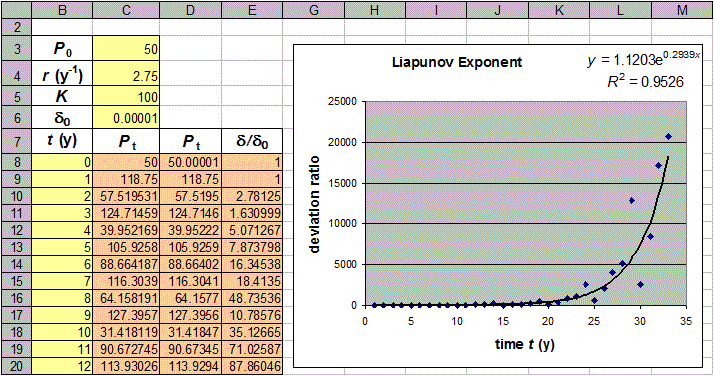
Para determinar se a razão, d/d0,
cresce exponencialmente, faz um gráfico de d/d0 contra o tempo e ajuste a curva exponencial aos dados. O
expoente, l, é o expoente de Liapunov, uma medida quantitativa de caos. Um valor de l menor ou igual a zero implica que o sistema não é caótico.
Faz um gráfico de d/d0
contra t. Agora adicione a linha de tendência exponencial. Escolha a opção para incluir a equação o valor de
R2 da linha de tendência no gráfico. Agora varie o valor da
taxa de crescimento, r, e determine o valor do expoente de Liapunov, l,
para valores diferentes de r.
|