|
Simnulação de um sistema predador-presa: Leão e Wildebeest

Começa com o modelo
de leão wildebeest
W t+1 = W t + rW
(1- W t/k) – K t
W = dinâmica da presa e K e a matança
L t+1 = L ts + Kta
A dinâmica do predador
= L, e s = sobrevivência e a+ assimilação
K = Wt (1-exp(-hLt))
A matança e um
menos a fração de sobreviventes da caça
h é a proporção de presas procuradas e encontradas por ano por cada predador
Use os parâmetros
seguintes
|
População
inicial de Wildebeest |
1.00E+06 |
|
Wilddebeest
r |
0.2 |
|
Wildebeest
k |
1500000 |
|
População
inicial de leões |
8000 |
|
Sobrevivência
dos leões |
0.8 |
|
|
|
|
|
|
|
Taxa
de matança |
0.000016 |
|
Leões
produzidos por wildebeest morto |
0.05 |
Clique aqui para baixar a planilha de respostas funcionais
Explore o comportamento
deste modelo ao mudar vários parâmetros. Em particular, determinar quais parâmetros
causam os ciclos serem exagerados e quais causam os ciclos a se apagaram..
Auto-regulação do predador
Vamos examinar
a auto-regulação do predador começando com a premissa que os leões são territoriais e existe um número máximo de leões de
1 ano de idade produzido no Serengeti. Podemos facilmente modelar essa condição
ao assumir que o número de recrutas leões (de 1 ano de idade) tem limite baseada no tamanho do território de um grupo de leões. Como uma forma funcional geral, começamos com a premissa
R t+1 = K t/(1/a + 1/C)K t
Onde R é o número de leões novos, previamente calculado simplesmente como aKt. Traze um gráfico dessa função usando o valor de a
superior a 0.05, e a c de 2000.
Explore o comportamento
do modelo mudando o parâmetro c.
Resposta funcional do Predador
Fixa o parâmetro
c=100,000 o que efetivamente
eliminará a auto-regulação do predador.
A equação
para a resposta funcional é
Na = T a pc N/1
+ (há pc N)
Temos como
premissas que os parâmetros são constantes
N é a densidade
de wildebeest/km*2
a’ é a área pesquisada por ano, ou seja 1460 km^2
pc é a probabilidade de ataque com êxito
h é o tempo
de manuseio, medido em anos e assim assume que um leão solitário leva 5 dias para comer um wildebeest, e por isso o tempo
de manuseio é 5/365
Agora
trocamos o modelo existente com uma resposta funcional.
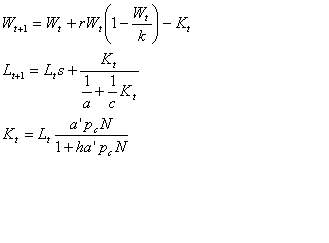 
Temos como premissas que os parâmetros são constantes
N é a densidade de wildebeest/km*2
a’ é a area pesquisada por ano, ou seja 1460 km^2
pc é a probabilidade de ataque com êxito
h é o tempo de manuseio, medido em anos e assim assume que um leão solitário leva 5 dias para
comer um wildebeest, e por isso o tempo de manuseio é 5/365
Como a resposta funcional afeita a dinâmica?
Calcule os isoclinais do predador e presa para o modelo sob a condição de auto-regulação e
compare o resultado com a resposta funcional do predador.
Redige seu relatório incorporando os gráficos e discussão usando
o artigo fornecido. Lembre as normas de apresentar o relatório. Você tem uma semana para fazer essa tarefa
Para o relatório lê e use o artigo:
John M. Fryxell,
Anna Mosser, Anthony R. E. Sinclair e Craig Packer (2007) Group formation stabilizes predator–prey dynamics.
Nature 449, 1041-1043
clique aqui para baixar o artigo
Lembre fazer um relatório detalhado interpretando suas simulações e o artigo!
Mande isso em separado para o e-mail da disciplina

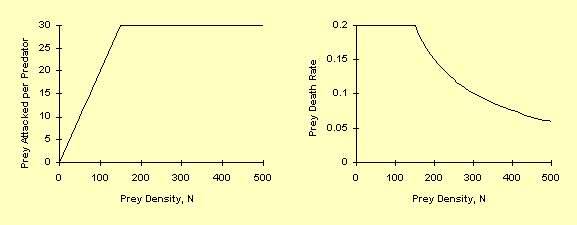
Tipos de Resposta Funcional
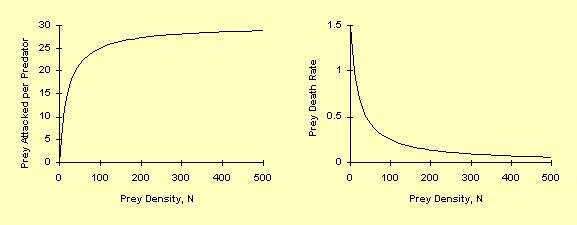
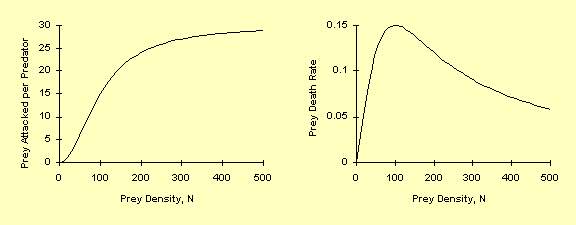
Tipo III
|



